Spline cubique

Une Spline créée dans TopSolid est une spline cubique non rationnelle.

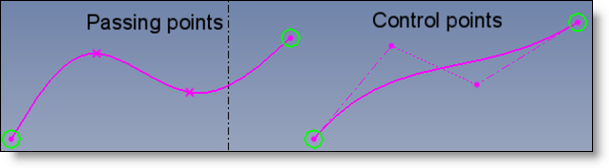
Une Spline est une courbe paramétrée par morceaux. Chaque morceau est un arc polynômial de degré 3. Les extrémités de chaque arc sont les points d’interpolation (également appelés points de passage).

Dans certains cas, il est pratique de définir la Spline, par des points d’attraction, également appelés points de contrôle.

La représentation de Bezier

La Spline est convertie et affichée comme une courbe de Bezier cubique non rationnelle, qui est une représentation plus géométrique du même objet.

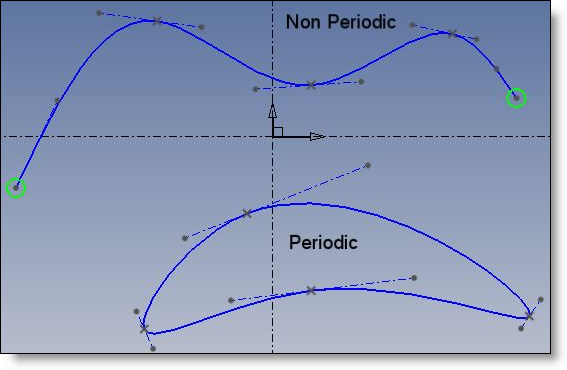
La courbe de Bezier cubique est définie par ses points de contrôle, numérotés de 0 à n. Les points modulo 3 (0, 3, 6, …) sont les points d’interpolation. Les autres sont les extrémités des tangentes à droite et à gauche aux points d’interpolation.

Chaque objet géométrique possède une dimension, ou plus simplement des degrés de liberté (Dof : « degree of freedom » en anglais). Ce nombre est le nombre de contraintes élémentaires indépendantes qu’il faut fixer pour fixer l’objet lui-même.

Si NbI est le nombre de points d’interpolation (début et fin compris dans le cas non périodique), et NbP est le nombre de points de Bézier, on a :

Continuité

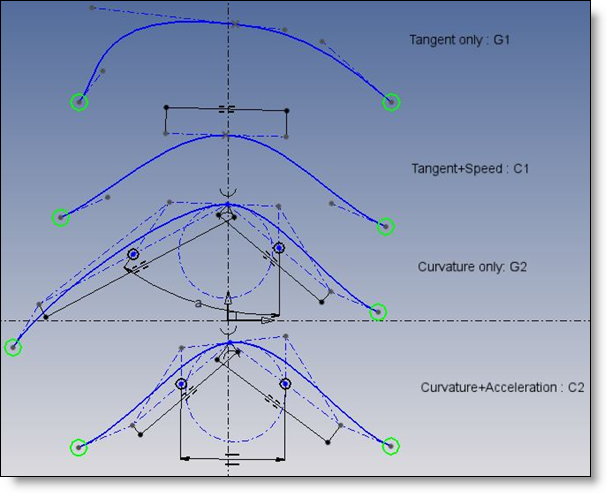
En un point d’interpolation, la courbe peut être plus ou moins continue. En imaginant que vous êtes un robot marchant le long de la courbe, et obéissant aux ordres de votre contrôleur (contraintes), les différents niveaux de continuité signifient :

- G0 ou position: les arcs sont connectés et vous ne pouvez tomber dans un trou ! Le nombre de contraintes additionnelles, Nbc, est nul.

- G1 ou Tangence: la direction de la vitesse (tangence) évolue continûment:  Nbc = 1

- C1 ou Tangence et vitesse: la vitesse évolue continûment en direction et module: Nbc = 2

- G2 ou Courbure: de plus, l’accélération normale évolue continûment. Le cercle osculateur est le même à droite et à gauche d’un point d’interpolation: Nbc = 3.

- C2 ou Courbure et accélération: de plus, l’accélération tangentielle ne comporte pas de saut (« jerk »).  Les composantes normales et tangentielles de l’accélération restent proportionnelles à droite et à gauche : Nbc=4

Tension

La courbe BSpline (Bezier spline) peut être tendue ou non. Imaginez que c’est une corde (sans élasticité le long de la tangente à la courbe) passant par des clous, et que vous tiriez aux extrémités, la corde prendra une forme qui maximisera l’énergie de la courbe, en minimisant sa courbure (1/R). Entre deux points, la courbe sera une ligne. Entre plusieurs points non alignés, la courbe prendra une forme « tendue ».

Quand un point d’interpolation est fixé et que la courbe est tendue, la courbe perd (3+1) Dof. Nous avons ainsi pour la courbe toute entière:

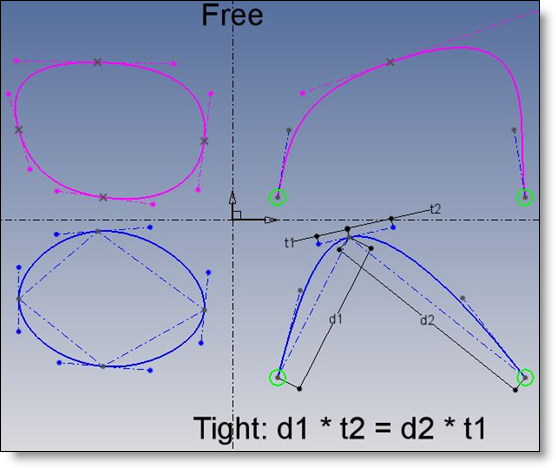
Remarques importantes dans le cas “tendu”:

- Quand la courbe est périodique, la courbe est totalement contrainte par ses points d’interpolation

- Dans le cas non périodique, on peut encore fixer les tangences au départ et à l’arrivée!

- La courbe est C2 lorsque l’option tendue est appliquée

- Une courbe tendue n’est pas appropriée pour le dessin de formes « molles »: on ne peut pas régler la courbure. La seule façon est d’ajouter encore plus de points d’interpolation.

Courbe libre (non tendue)

La courbe est G2 par défaut quand elle n’est pas tendue. La courbe perd 3 Dof (degrés de liberté « degree of freedom » en anglais) en chaque point d’interpolation qui est fixé.

Remarques:

Quand la courbe est périodique, on garde seulement 2 Dof en chaque point d’interpolation. Ce n’est pas assez pour permettre de bouger localement une tangente en gardant les autres intactes. Lorsque l’on bouge (Drag) une tangente en bout, les autres tangentes bougent, en cherchant à préserver leur direction.

Pour forcer les tangentes à garder leur direction, on doit utiliser le Alt+Drag mode.

La situation est « pire » dans le cas C2. Bouger une tangence implique que toutes les autres tangences bougeront en module et direction.

C’est une bonne raison pour choisir le mode G2 comme mode par défaut.

Courbure

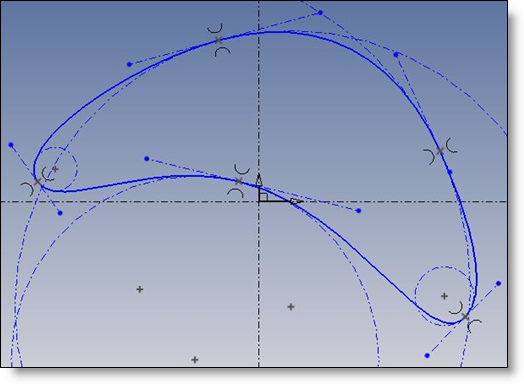
Lorsque la courbe est G2 continue (cas standard), et les points d’interpolation et les cercles osculateurs sont fixés, la courbe est totalement contrainte dans le cas périodique.

Dans le cas non périodique, la courbe garde 2 Dof (degrés de liberté « degree of freedom » en anglais) et garde des degrés de liberté en bout (tangentes de début et de fin).

Dans le cas C2, la courbe est « surcontrainte » et peut ne pas se résoudre.

Les contraintes

ASpline cubique

On peut créer des courbes BSpline plus évoluées, appartenant toujours à la catégorie des courbes par morceaux polynomiales cubiques, mais cette fois ci avec un dénominateur (courbe rationnelle).

L’intérêt majeur est que cela permet de représenter parfaitement les cercles et arcs de coniques (ellipse, parabole, hyperbole), comme des arcs de Bezier contrôlés de la même façon par des points de contrôle : tous les types de courbe usuels sont couverts (ASpline veut dire « A(ll)Spline » !).

Types d’arcs

Chaque arc de la courbe, qui est une liste d’arcs contigus, a un type correspondant aux types géométriques usuels.

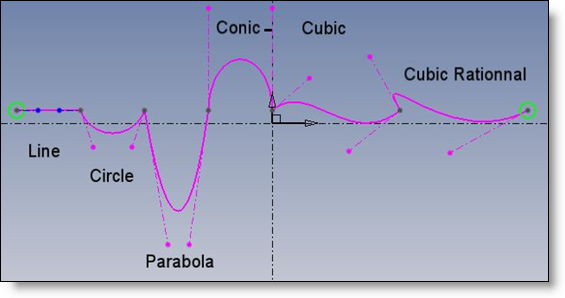
La ligne est de degré 1: pas de courbure

Le cercle, la parabole et la conique (ellipse, hyperbole) sont de degrés deux : ce sont des courbes convexes (pas de possibilité de traverser la tangente) sans point d’inflexion. La courbure garde toujours le même signe.

L’arc cubique ou rationnel cubique est de degré 3 : la courbe peut traverser sa tangente.

Types de point d’interpolation

En chaque point d’interpolation, on peut prescrire un type de continuité :

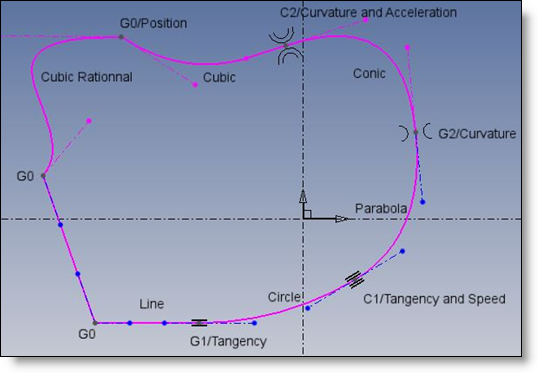
Si un point suit la courbe avec une certaine vitesse et accélération, en suivant le paramétrage de la courbe, il peut changer de direction, courbure, vitesse et accélération en chaque point d’interpolation.

G0 continu: tout peut changer, sauf la continuité

G1 continu: la direction est conservée

C1 continu: direction et vitesse sont conservées

G2 continu: direction, vitesse et courbure sont conservées

C2 continu: direction, vitesse, courbure et accélération sont conservées

La « douceur » de la courbe augmente graduellement de G0 à C2.

Exemples