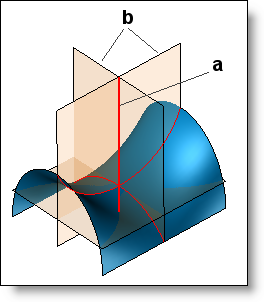
S'il est relativement simple de définir le rayon de courbure d'une courbe plane, pour une surface les choses se compliquent. On définit alors un analogue comme suit : en un point, on définit un axe, le vecteur normal à la surface (a).
On imagine ensuite un plan tournant sur cet axe. Ce plan intersecte la surface considérée en une courbe. Il permet donc de définir une infinité de rayons de courbure.
Parmi ces rayons, on choisit les rayons de courbure minimum et maximum. Ils définissent des courbures maximale et minimale. On les appelle les courbures principales, et les plans contenant ces courbures sont représentés ci-dessous (b).
Les courbures principales sont donc les courbures, au point considéré, des deux courbes rouges intersections de ces plans et de la surface.
La courbure moyenne est définie comme la moyenne de ces deux courbures.
La courbure de Gauss est définie par le produit de ces deux courbures.