Fixed count:

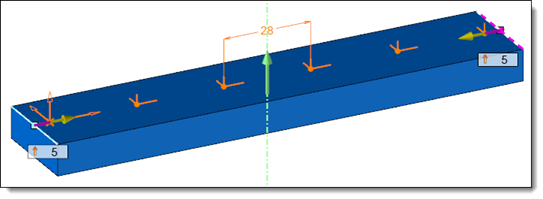
The number of instance Nb is given by the user.
The distance d between each instance is equal to: (D - (d1 + d2)) / (Nb - 1)
Example of distribution between 2 points with fixed count and start and end margin.
D = 150mm, d1 = d2 = 5mm and Nb = 6
So the result is d = (150 - (5 + 5)) / (6 - 1)) = 28mm
Maximum distance:
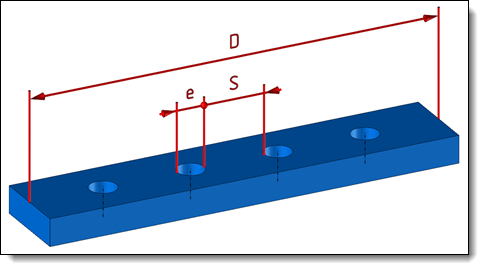

The maximum spacing Smax and the thickness e are given by the user.
The computation of the effective spacing S is made according to the following way:
-
First, we start by computing the number of instance Nb = (D - Smax) / (Smax + e)
This result is rounded to the upper integer.
-
Then, the effective spacing S is equal to: (D - (Nb x e)) / (Nb + 1)
Example of distribution between 2 points with maximum spacing and thickness (orange circles in dotted line).
D = 150mm, Smax = 24mm and e = 6mm
It gives: Nb = (150 - 24) / (24 + 6) = 4,2
Then Nb is rounded to 5 and S = (150 - (5 x 6) / (5 + 1) = 20mm
Step:
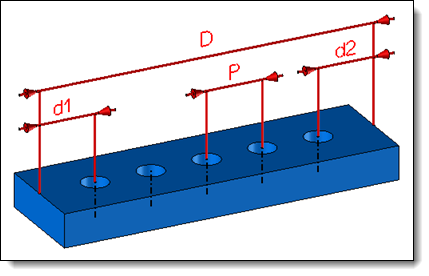
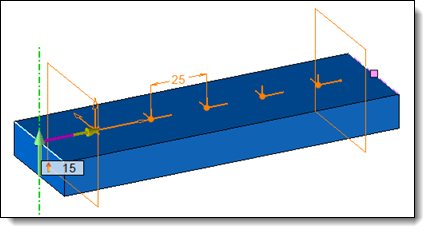
The distance between occurrences (P) and the minimum margins (d1 and d2) are given by the user.
-
First, we start by computing the number of intervals N = D - (d1 + d2) / P
This result is rounded to the lower integer.
-
The number of occurrence is equal to N + 1
Example of distribution between 2 points with a step and equal start and end minimum margins.
D = 150mm, P = 25mm and d1 = d2 = 15mm
It gives: N = 150 - (15 +15) / 25 = 4,8
Then N is rounded to 4 and the number of occurrence is equal to 5.
Unit Step:
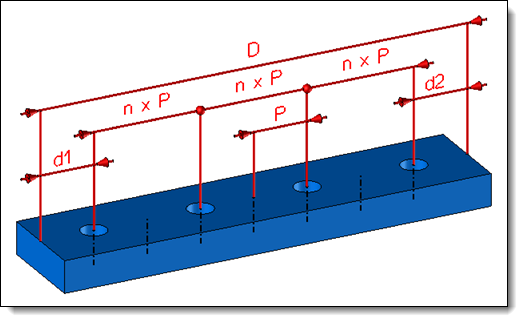
The minimum distance between occurrences (Unit Step), the number of occurrences Nb and the minimum margins (d1 and d2) are given by the user.
-
First, we start by computing the theorical interval N = D - (d1 + d2) / Nb - 1
-
Then, we try to find if the theorical interval is a multiple of Nb in order to the highest possible step value.
Example of distribution between 2 points with a unit step and equal start and end minimum margins.
D = 200mm, P = 25mm, N = 4 and d1 = d2 = 15mm
It gives: N = 200 - (15 +15) / (4 - 1) = 56.66
N is a multiple of the unit step, then the step becomes 2 x 25mm