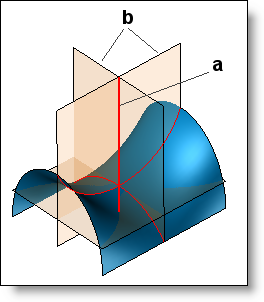
It is quite simple to define the curvature radius of a planar curve, but for a surface, things get more complex. We can define an analog as follow: on a point, we define an axis which is the normal vector to the surface (a).
Then, imagine a plane spining around this axis. This plane intersect the surface and a curve can be deduced from this intersection. So this plane allows to get an infinite quantity of curvature radii.
Among these curvature radii, we choose the maximum and minimum radius. They define the minimum and maximum curvature. The are called main curvature, and the plane that contains these curvatures are represented on the picture (b).
So the main curvature are the curvature, on the given point, of the two red curves resulting of the intersection between the planes and the surface.
The mean curvature is defined by the mean of the two main curvature.
The Gaussian curvature is define by the product of the mean curvature.