Kubischer Spline

Wenn Sie einen Spline mit TopSolid erstellen, handelt es sich dabei um einen nicht rationalen kubischen Spline (Grad 3).

Ein Spline ist eine (kubische) polynominale ununterbrochene Kurve, die als Liste angrenzender Bögen segmentiert wird. Die Bogenendpunkte sind Interpolationspunkte (auch Durchgangspunkte genannt).

In einigen Fällen kann es nützlich sein, den Spline durch Anziehungspunkte, auch so genannte Kontrollpunkte, zu definieren.

Bezier-Darstellung

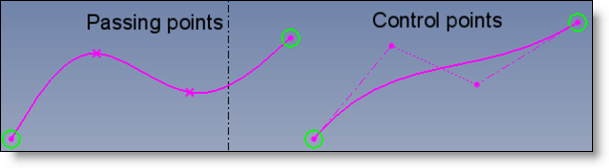
Der kubische BSpline wird als nicht rationale kubische Bezier-Kurve umgewandelt und angezeigt, wobei es sich um eine geometrischere Darstellung desselben mathematischen Objekts handelt.

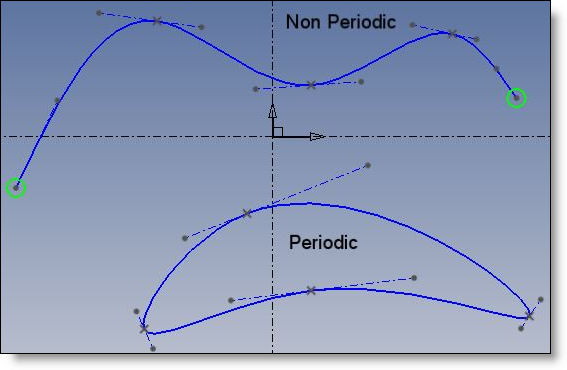
Eine kubische Bezier-Kurve wird durch ihre Kontrollpunkte bestimmt, die von 0 bis n nummeriert sind. Die Ternären sind die Interpolationspunkte. Die anderen sind die Endpunkte der linken und rechten Tangenten.

Jedes geometrische Objekt hat eine mathematische Bemaßung oder einen Freiheitsgrad (Dof). Diese Zahl steht für die Anzahl grundlegender Zwangsbedingungen (Fixierung eines Freiheitsgrads), die Sie festlegen müssen, wenn das Objekt fixiert wird.

NbI steht für die Anzahl von Interpolationspunkten (einschließlich Anfang und Ende im nicht periodischen Fall) und NbP für die Anzahl von Bezier-Punkten.

Kontinuität

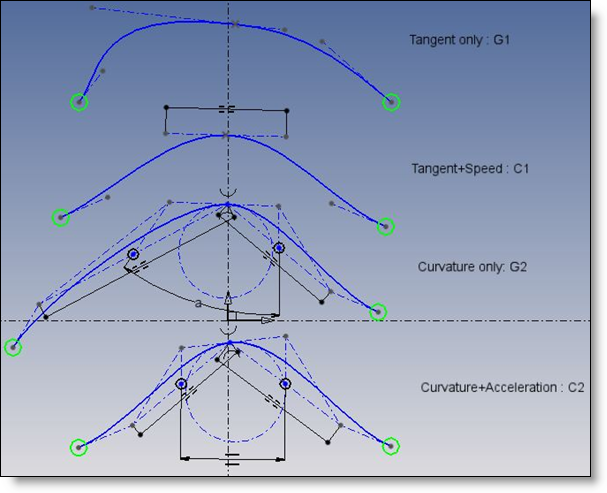
An einem Bezier-Interpolationspunkt kann die Kurve mehr oder weniger glatt sein. Stellen Sie vor sich, ein Roboter würde entlang der Kurve laufen mit einer Geschwindigkeit, die von einem (guten!) Meister irgendwo vorgeschrieben wird. Unterschiedliche Stetigkeitsgrade:

- G0 oder angeschlossen: keine zusätzliche Zwangsbedingung auf einen Interpolationspunkt. Dasselbe gilt links und rechts! Anzahl zusätzlicher Zwangsbedingungen, Nbc, ist null.

- G1 oder Tangente: die Geschwindigkeitsrichtung bleibt gleich: Nbc = 1

- C1 oder Tangente und Geschwindigkeit: der Geschwindigkeitsvektor bleibt gleich (linke und rechte Tangenten bleiben proportional oder gleich): Nbc = 2

- G2 oder Krümmung: neben C1 behält die normale Beschleunigung die gleiche Richtung bei, was mit den Krümmungsmittelpunkten übereinstimmt, oder der Schmiegungskreis ist links und rechts gleich: Nbc = 3

- C2 oder Krümmung und Beschleunigung: Die tangentiale Beschleunigung hat links und rechts die gleichen Proportionen wie die normale: Nbc=4

Enge

Das BSpline (Bezier Spline) kann fest sein oder nicht. Stellen Sie vor sich, dass eine Spline ein klassisches Seil ist (keine Elastizität entlang seiner Tangente) das entlang vorgeschriebener Punkt (Klammern) verläuft. Und das Sie an dem Seil ziehen oder drücken können. Wenn Sie so fest ziehen, wir Sie können, nimmt die Schnur eine bestimmte Form an. Diese Form maximiert die Seilenergie und minimiert die Krümmung (= 1 / Radius) entlang der Kurve. Zwischen zwei Punkten ist die Schnur in eine Linie geformt. Zwischen mehreren Punkten nimmt die Leitung eine feste Form an, weil diese nicht ausgerichtet sind und die Krümmungskontinuität bewahrt wird.

Wenn ein Interpolationspunkt fixiert ist und die Kurve eng ist, verliert die Kurve (3+1) Dof. Für die gesamte Kurve gilt:

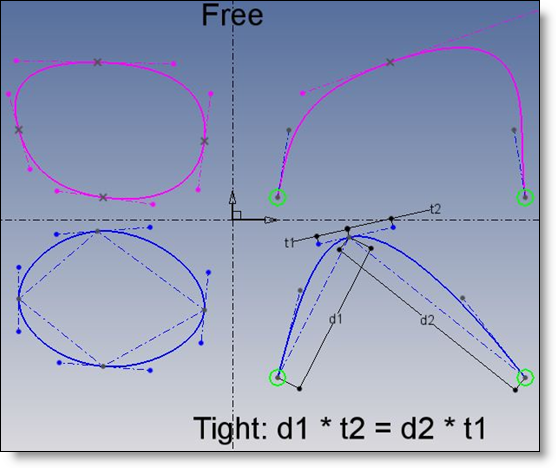
Wichtige Anmerkungen: "Enger Fall":

- Wenn periodisch, ist die Kurve gut bedingt.

- Wenn nicht periodisch, können die Start- und Endtangenten noch fixiert werden!

- Die Kurve wird automatisch auf C2 eingestellt, wenn die enge Option in TopSolid verwendet wird

Die Kurve ist angespannt und diese ist nicht gut, um ungeformte Formen zu entwerfen: die Krümmung kann nicht fein abgestimmt werden. Die einzige Möglichkeit besteht dann darin, immer mehr Interpolationspunkte hinzuzufügen.

Freier Fall

Wenn die Kurve nicht angezogen wird, ist die Kurve G2, und die Interpolationspunkte sind fixiert, die Kurve verliert 3 Dof pro Interpolationspunkt:

Anmerkungen:

Wenn periodisch, werden nur zwei Dof an jedem Interpolationspunkt aufbewahrt. Es reicht nicht aus, eine Tangente lokale verschieben zu dürfen, während die andere fixiert bleibt. Wenn Sie daher einen Tangentenendpunkt ziehen, verschieben sich die anderen Tangenten etwas in Länge und Richtung und versuchen, ihre Richtung zu halten.

Um die anderen Tangenten "mehr" zu zwingen, ihre Richtung beizubehalten und sie nur in der Länge anzupassen, müssen Sie den Alt+Ziehen-Modus verwenden.

Die Situation ist im Fall C2 "schlechter". Eine Tangente zu verschieben, bedeutet alle Tangenten zu verschieben, ohne ihre Richtungen beibehalten zu können.

Es ist ein triftiger Grund, G2 als Standard-BSpline-Fall zu wählen.

Krümmung

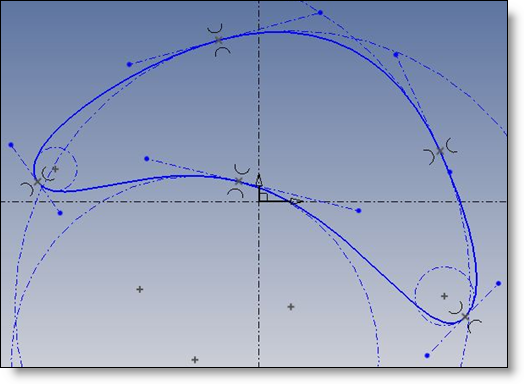
Wenn die Kurve G2-durchgängig (allgemeiner Fall) ist, und der Interpolationspunkt sowie Schmiegungskreis fixiert sind, ist die Kurve im periodischen Fall gut beschränkt. Bemerkenswerte Eigenschaft.

Im nicht periodischen Fall bewahrt die Kurve 2 Dof, und Sie müssen die Länge der Start-/Endtangenten noch fixieren.

Im Fall C2 ist die Kurve übermäßig begrenzt und kann möglicherweise nicht gelöst werden.

Die Zwangsbedingungen

Kubischer ASpline

Es gibt einen Weg, um höher entwickelte Kubik-BSplines zu erstellen, die immer zur Kategorie der polynominalen kubischen Kurve gehören, aber womöglich mit einem rationalen Nenner (Kubisch rationales Bezier).

Das Interessant ist, dass es eine perfekt Darstellung von Kreisen, Kegeln, Parabelkurven als Bezier-ähnliche Kurve, die durch Punkte gesteuert wird, ermöglicht: es kann alle üblichen Kurven darstellen. ASpline bedeutet A(ll)Spline!

Bogentypen

Jeder BSpline, der eine Liste von angrenzenden polynominalen Bögen ist, hat einen Typ entsprechend den üblichen geometrischen Bögen:

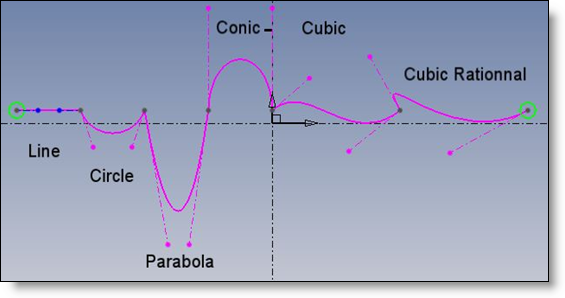
Die Linie ist Grad 1: keine Krümmung

Der Kreis, die Parabel, konische Bögen sind Grad 2: sie sind konvexe Bögen ohne Wendepunkte. Krümmung hat immer das gleiche Zeichen.

Kubisch und Kubisch Rational sind Grad 3: die Kurve kann ihre Tangente werfen.

Scheitelpunkttypen

An jedem Scheitelschnittpunkt von zwei angrenzenden Bögen können Sie eine Kontinuitätseigenschaft definieren:

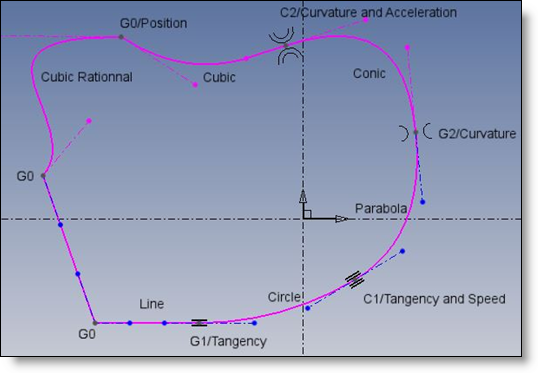
Wenn ein Punkt der Kurve mit einer bestimmten Geschwindigkeit und Beschleunigung folgt, kann er gemäß der Kurvenparametrisierung die Richtung, Krümmung, Geschwindigkeit, Beschleunigung an jedem ASpline-Scheitelpunkt ändern.

G0-Kontinuität: alles kann am Scheitelpunkt geändert werden, mit Ausnahme der Scheitelpunktposition

G1-Kontinuität: Richtung wird beibehalten

C1-Kontinuität: Richtung und Geschwindigkeit werden beibehalten

G2-Kontinuität: Richtung, Geschwindigkeit, Krümmung werden beibehalten

C2-Kontinuität: Richtung, Geschwindigkeit, Krümmung, Beschleunigung werden beibehalten

Die Kurvenglattheit erhöht sich von G0 auf C2.

Beispiele